[笔记]非线性自适应控制器设计，对应对应DR_CAN老师的【Advanced控制理论】16

简单的自适应控制器设计，使用李雅普诺夫函数证明系统稳定性后解出对应的控制输入u，对应DR_CAN老师的【Advanced控制理论】16

$\dot{x}=a{x}^2+u$$\dot{x}=a{{x}^{2}}+u$

其中$x$$x$是系统状态，$a$$a$为参数，$u$$u$为系统输入。

设置期望状态$x_d$${{x}_{d}}$，状态误差为$e=x_d-x(2)$$e={{x}_{d}}-x\text{ }(2)$，控制目标为$e\to 0$$e\to 0$

一、假设参数$a$$a$为已知量

对(2)式求导后为：

$\dot{e}={\dot{x}}_d-\dot{x}={\dot{x}}_d-a{x}^2-u(3)$$\dot{e}={{\dot{x}}_{d}}-\dot{x}={{\dot{x}}_{d}}-a{{x}^{2}}-u\text{ }(3)$

设计Lyapunov函数为（易知式（4）为PD（正定））：

$V_{(e)}=\frac{1}{2}{e}^2(4)$${{V}_{(e)}}=\frac{1}{2}{{e}^{2}}\text{ }(4)$

对(4)求导并把(3)带入得：

${\dot{V}}_{(e)}=e\dot{e}=e({\dot{x}}_d-a{x}^2-u)(5)$${{\dot{V}}_{(e)}}=e\dot{e}=e({{\dot{x}}_{d}}-a{{x}^{2}}-u)\text{ }(5)$

为了满足${\dot{V}}_{(e)}$${{\dot{V}}_{(e)}}$为ND（负定），设${\dot{x}}_d-a{x}^2-u=-ke$${{\dot{x}}_{d}}-a{{x}^{2}}-u=-ke$，

此时，${\dot{V}}_{(e)}=-k{e}^2$${{\dot{V}}_{(e)}}=-k{{e}^{2}}$，显然此时L导数为负定，即满足系统稳定性的条件。

由此可以得出控制输入为：

$u={\dot{x}}_d-a{x}^2+ke(6)$$u={{\dot{x}}_{d}}-a{{x}^{2}}+ke\text{ }(6)$

仿真参考[Advance控制理论]简单的反步控制器设计

二、假设参数$a$$a$为未知量

如一中假设参数$a$$a$为已知量，但一般参数$a$$a$都是未知量即一个缓慢变化的常数（例如一个机械臂需要抓取不同质量的物体，那么这个质量就是一个短时间不会变化的常数，此时$\dot{a}=0$$\dot{a}=0$）。

此时同样设状态误差$e=x_d-x\text{ (2)}$$e={{x}_{d}}-x\text{ (2)}$，

$\dot{e}={\dot{x}}_d-\dot{x}={\dot{x}}_d-a{x}^2-u(3)$$\dot{e}={{\dot{x}}_{d}}-\dot{x}={{\dot{x}}_{d}}-a{{x}^{2}}-u\text{ }(3)$

因为参数$a$$a$为未知量，此时需要系统估计该值，设估计值为$\hat{a}$$\widehat{a}$

估计误差的导数为：$\stackrel{\cdot }{\tilde{a}}=\dot{a}-\stackrel{\cdot }{\hat{a}}$$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widetilde{a}}}\,=\dot{a}-\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,\text{ }$，其中$\dot{a}=0$$\dot{a}=0$

$\stackrel{\cdot }{\tilde{a}}=-\stackrel{\cdot }{\hat{a}}\text{ (7)}$$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widetilde{a}}}\,=-\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,\text{ (7)}$

此时设计Lyapunov函数(PD)为：

$V_{(e,a)}=\frac{1}{2}{e}^2+\frac{1}{2}{\tilde{a}}^2(8)$${{V}_{(e,a)}}=\frac{1}{2}{{e}^{2}}+\frac{1}{2}{{\widetilde{a}}^{2}}\text{ }(8)$

对(8)求导并带入(3)与(7)得：

${\dot{V}}_{(e,a)}=e({\dot{x}}_d-a{x}^2-u)-\tilde{a}\stackrel{\cdot }{\hat{a}}(9)$${{\dot{V}}_{(e,a)}}=e({{\dot{x}}_{d}}-a{{x}^{2}}-u)-\widetilde{a}\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,\text{ }(9)$

为了满足(9)为负定，设$u={\dot{x}}_d-\hat{a}{x}^2+ke(10)$$u={{\dot{x}}_{d}}-\widehat{a}{{x}^{2}}+ke\text{ }(10)$

将(10)带入(9)得：

${\dot{V}}_{(e,a)}=-k{e}^2-\tilde{a}(e{x}^2+\stackrel{\cdot }{\hat{a}})(11)$${{\dot{V}}_{(e,a)}}=-k{{e}^{2}}-\widetilde{a}(e{{x}^{2}}+\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,)\text{ }(11)$

易知，$-k{e}^2$$-k{{e}^{2}}$为ND，若令$\stackrel{\cdot }{\hat{a}}=-e{x}^2$$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,=-e{{x}^{2}}$，此时${\dot{V}}_{(e,a)}=-k{e}^2$${{\dot{V}}_{(e,a)}}=-k{{e}^{2}}$为NSD(半负定)。

引入引理1：假设

①$V\ge 0$$V\ge 0$

②$\dot{V}<-g(t)(g(t)\ge 0)$$\dot{V}<-g(t)\text{ }(g(t)\ge 0)$且$\dot{g}(t)\in L_{\mathrm{\infty }}$$\dot{g}(t)\in {{L}_{\infty }}$

那么$g(t)$$g(t)$有界，即$\underset{t\to \mathrm{\infty }}{lim}g(t)=0$$\underset{t\to \infty }{\mathop{\lim }}\,g(t)=0$

由引理1知，式(11)在设$\stackrel{\cdot }{\hat{a}}=-e{x}^2$$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,=-e{{x}^{2}}$情况下满足李雅普诺夫稳定条件。

$\hat{a}=-{\int }_0^{t}e{x}^{2}dt$$\widehat{a}=-\int_{0}^{t}{e{{x}^{2}}dt}$

最终得控制输入$u$$u$为：

$u={\dot{x}}_d+x^2{\int }_0^{t}e{x}^{2}dt+ke(12)$$u={{\dot{x}}_{d}}+{{x}^{2}}\int_{0}^{t}{e{{x}^{2}}dt}+ke\text{ }(12)$

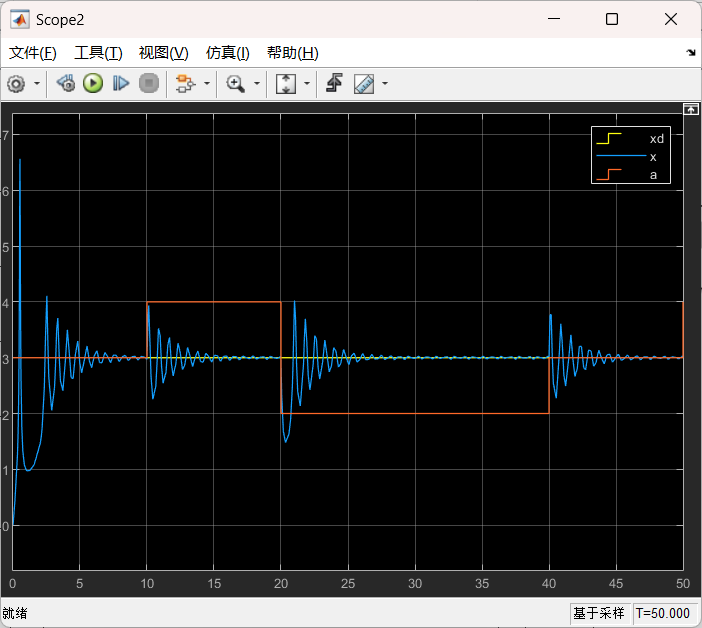
Matlab/Simulink仿真为：

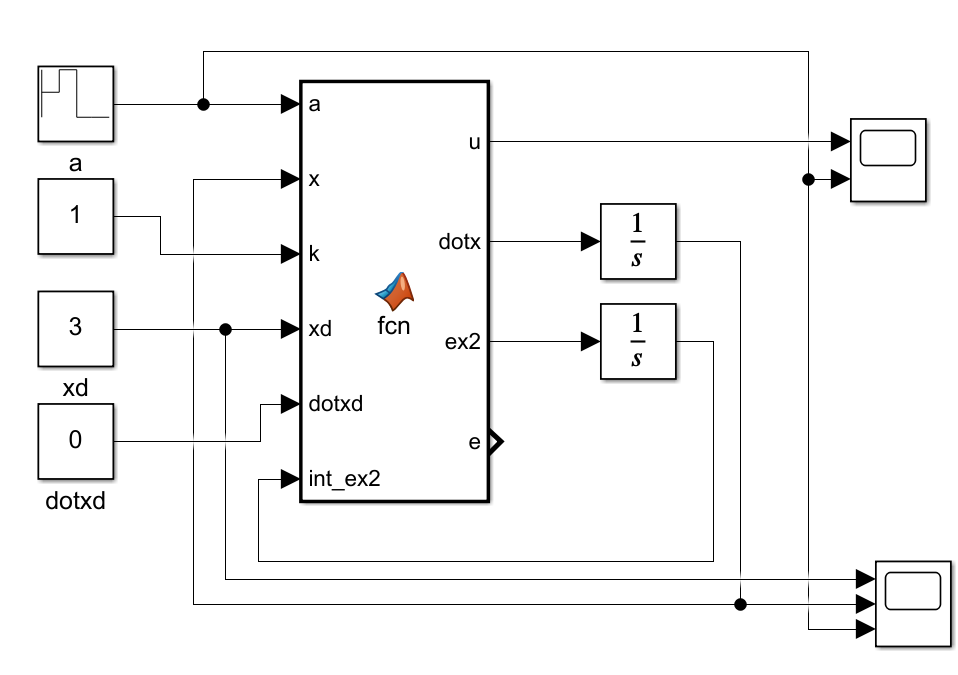
xxxxxxxxxx
function [u, dotx, ex2, e] = fcn(a, x, k, xd, dotxd, int_ex2)
%#codegen
e = xd - x;
ex2 = e*x^2;
u = dotxd + int_ex2*x^2 + k*e;
dotx = a*x^2 + u;

在不知道参数$a$$a$的情况下，$\hat{a}$$\widehat{a}$可以很好的估计参数值。

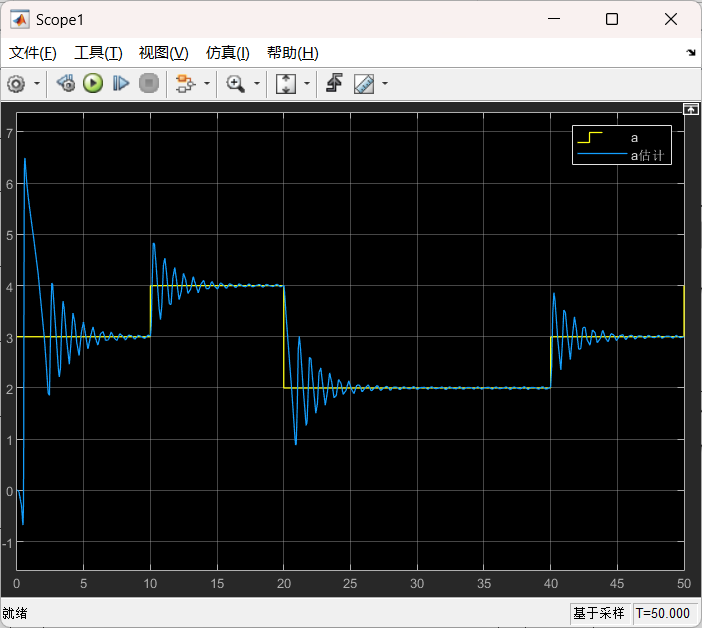
在目标状态$x_d$$x_d$不变的情况下，未知参数$a$$a$的改变会使控制输入经历一段时间的调整后$e\to 0$$e\to 0$。