第三部分的自适应控制学习，对应前两部分的强化。为为弹簧系统设计控制器满足弹性系数未知的情况下通过控制输入u使得系统到达指定位置

其一：Advance控制理论简单的反步控制器设计

其二：从零学使用Lypunov直接法设计自适应控制器

其三：在弹性系数未知的情况下设计自适应控制器

系统方程为：$m\ddot{x}+\partial x^3=F(1)$$m\ddot{x}+\partial {{x}^{3}}=F\text{ }(1)$​

由于博客对lateX容忍度不高，即便我开启了数学公式解析，所以想更舒服的观看的点击这里

其中$m$$m$为方块的质量，$x$$x$为方块的位移，$\partial$$\partial$为未知弹性系数，$F$$F$为输入量。

转换为动态方程为：

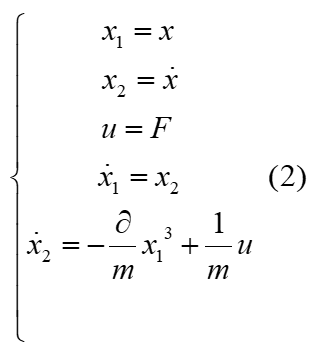
控制目标：在$\partial$$\partial$未知的情况下，使得方块系统状态$x\to x_d$$x\to {{x}_{d}}$，其中$x_d$${{x}_{d}}$为期望状态。

设状态误差分别为：

$e=x_{1d}-x_1(3)$$e={{x}_{1d}}-{{x}_{1}}\text{ }(3)$

$r=x_{2d}-x_2(4)$$r={{x}_{2d}}-{{x}_{2}}\text{ }(4)$

$\tilde{\partial }=\partial -\hat{\partial }(5)$$\widetilde{\partial }=\partial -\widehat{\partial }\text{ }(5)$

其中$e$$e$、$r$$r$为系统状态误差，$\tilde{\partial }$$\widetilde{\partial }$为弹性参数估计误差，$\hat{\partial }$$\widehat{\partial }$为估计弹性参数。

首先设计李雅普诺夫函数为：

$V_{(e,r)}=\frac{1}{2}{e}^2+\frac{1}{2}{r}^2\text{ (PD) }(6)$${{V}_{(e,r)}}=\frac{1}{2}{{e}^{2}}+\frac{1}{2}{{r}^{2}}\text{ (PD) }(6)$

${\dot{V}}_{(e,r)}=e\dot{e}+r\dot{r}(7)$${{\dot{V}}_{(e,r)}}=e\dot{e}+r\dot{r}\text{ }(7)$

为保证设计函数为稳定的必须满足李雅普诺夫设计函数为正定，一阶导数为负定。对函数(3)、(4)求导并带入(7)得：

${\dot{V}}_{(e,r)}=e({\dot{x}}_{1d}-{\dot{x}}_1)+r({\dot{x}}_{2d}-{\dot{x}}_2)(8)$${{\dot{V}}_{(e,r)}}=e({{\dot{x}}_{1d}}-{{\dot{x}}_{1}})+r({{\dot{x}}_{2d}}-{{\dot{x}}_{2}})\text{ }(8)$

为了满足上述条件设计：${\dot{x}}_{1d}-{\dot{x}}_1=-k_{1}e+r$${{\dot{x}}_{1d}}-{{\dot{x}}_{1}}=-{{k}_{1}}e+r$并带入(8)为：

${\dot{V}}_{(e,r)}=-k_{1}e+r(e+\dot{r})$${{\dot{V}}_{(e,r)}}=-{{k}_{1}}e+r(e+\dot{r})\text{ }$同时令$e\text{+}\dot{r}=-k_{2}r(9)$$e\text{+}\dot{r}=-{{k}_{2}}r\text{ }(9)$

对(9)式进行整理：

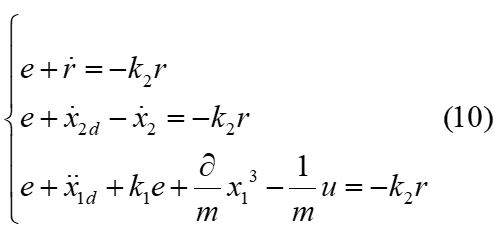
带$\tilde{\partial }$$\widetilde{\partial }$的李雅普诺夫函数设计为：

${\dot{V}}_{(e,r,\tilde{\partial })}=e\dot{e}+r\dot{r}+\tilde{\partial }\stackrel{\cdot }{\tilde{\partial }}(11)$${{\dot{V}}_{(e,r,\widetilde{\partial })}}=e\dot{e}+r\dot{r}+\widetilde{\partial }\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widetilde{\partial }}}\,\text{ }(11)$

将整理后的式(10)带入式(11)得：

${\dot{V}}_{(e,r,\tilde{\partial })}=-k_1{e}^2+r({\dot{x}}_{2d}-{\dot{x}}_2)-\tilde{\partial }\stackrel{\cdot }{\hat{\partial }}(12)$${{\dot{V}}_{(e,r,\widetilde{\partial })}}=-{{k}_{1}}{{e}^{2}}+r({{\dot{x}}_{2d}}-{{\dot{x}}_{2}})-\widetilde{\partial }\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{\partial }}}\,\text{ }(12)$

因为$\partial$$\partial$弹性系数位置，使用$\hat{\partial }$$\widehat{\partial }$估计参数，此时$u$$u$设为：

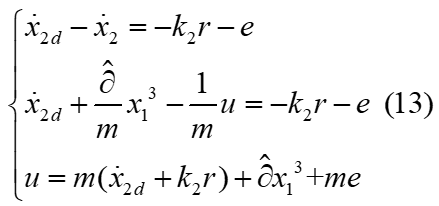
将(13)带入(12)得到

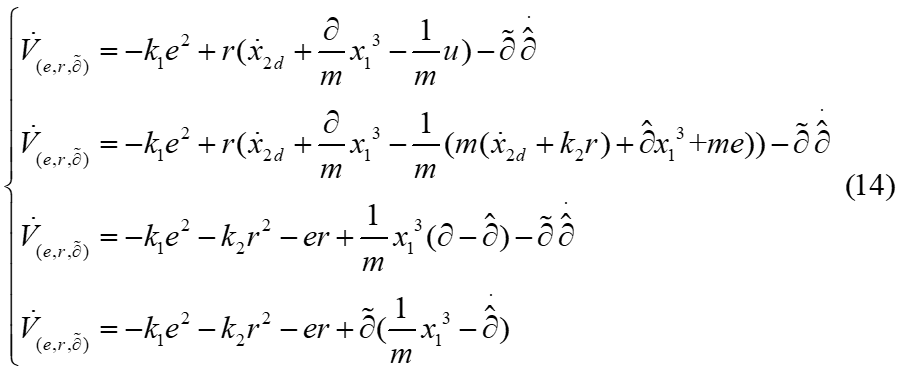
设$\stackrel{\cdot }{\hat{\partial }}=\frac{1}{m}{x_1}^3$$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{\partial }}}\,=\frac{1}{m}{{x}_{1}}^{3}$由引理1可证${\dot{V}}_{(e,r,\tilde{\partial })}$${{\dot{V}}_{(e,r,\widetilde{\partial })}}$为NSD(半负定)

综上，控制输入$u$$u$为：

$u=me+{\ddot{x}}_{1d}+k_1\dot{e}+\frac{1}{m}{x_1}^3{\int }_0^t{x_1}^{3}rdt+k_{2}r$$u=me+{{\ddot{x}}_{1d}}+{{k}_{1}}\dot{e}+\frac{1}{m}{{x}_{1}}^{3}\int_{0}^{t}{{{x}_{1}}^{3}rdt}+{{k}_{2}}r$

Matlab/Simulink仿真

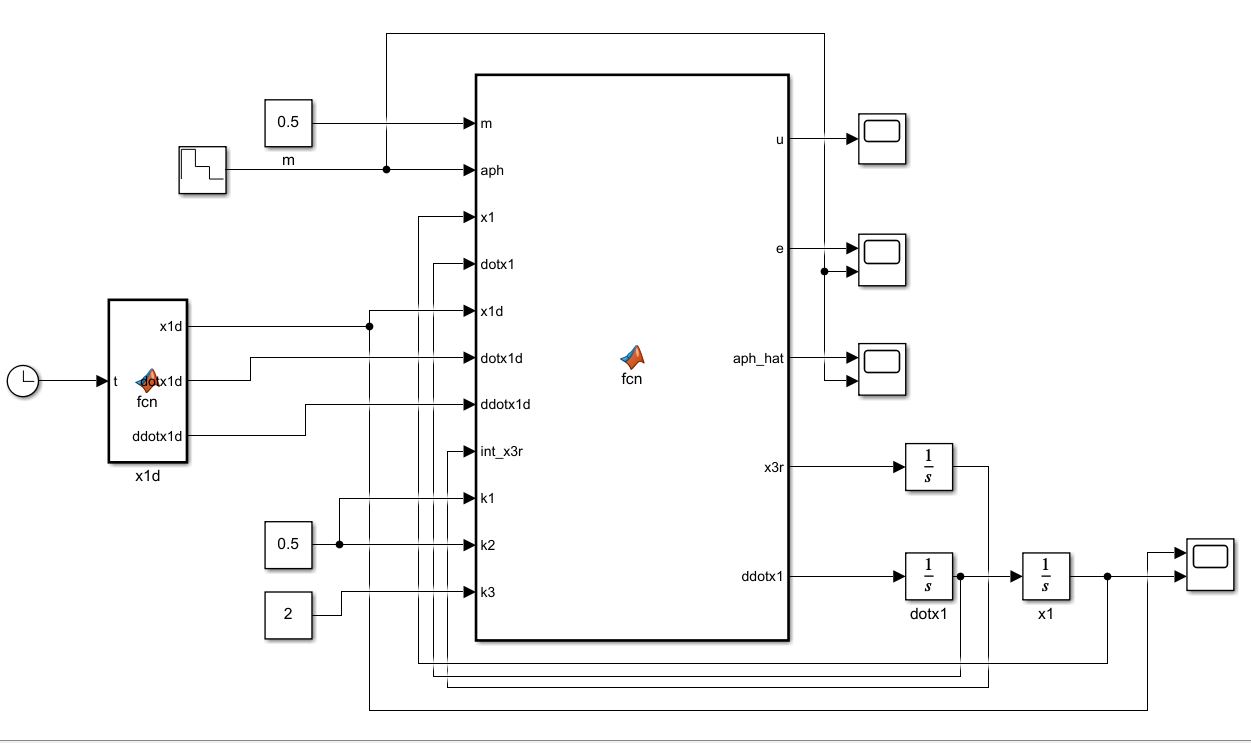
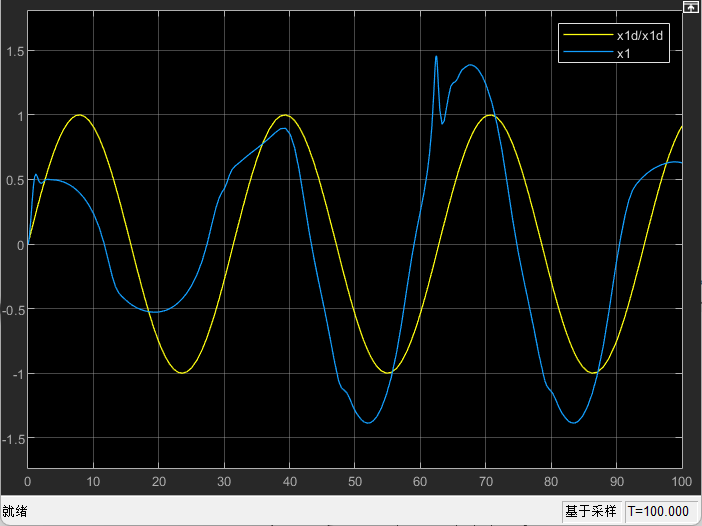
懒得描述啦，看结果吧

[photo]

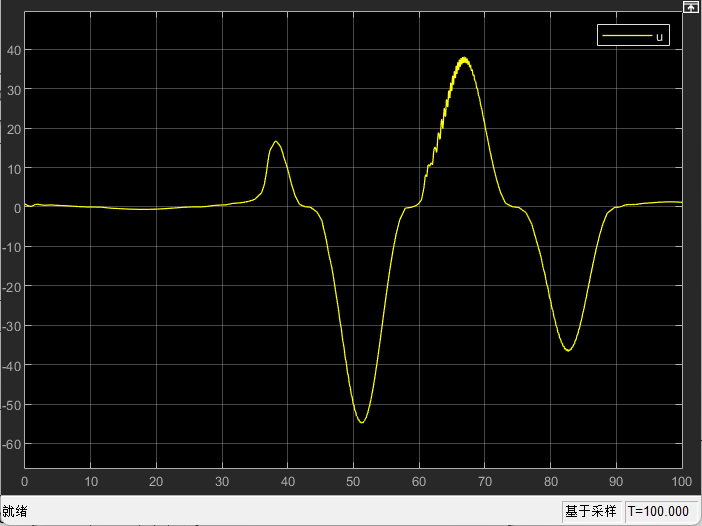
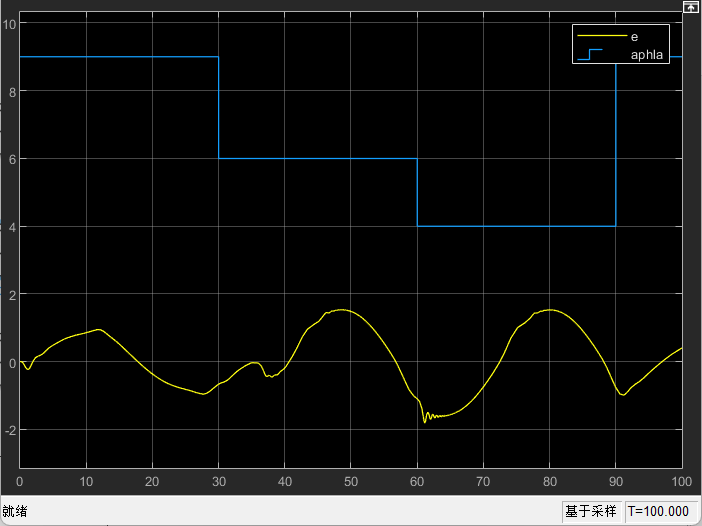
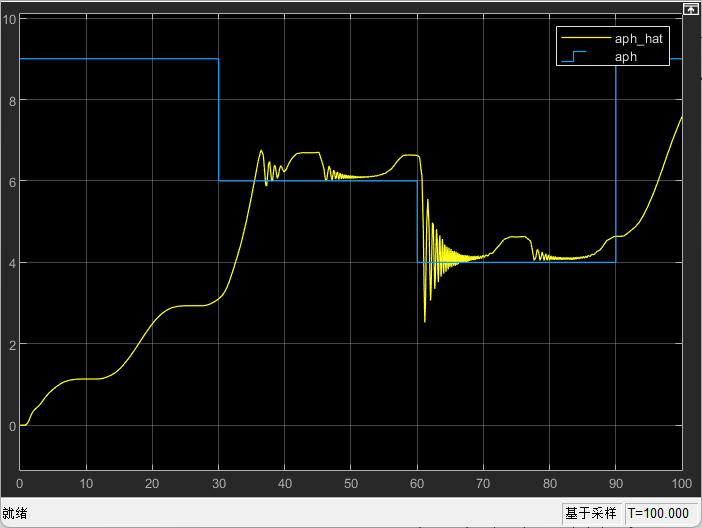
[/photo]

调节不同的k1,k2,k3应该会让效果更好，可以动手试一下

源码如下

xxxxxxxxxx
function [u, e, aph_hat, x3r, ddotx1] = fcn(m, aph, x1, dotx1, x1d, dotx1d, ddotx1d, int_x3r, k1, k2, k3)

e = x1d - x1;
x2d = dotx1d + k1*e;
r = x2d - dotx1;
x3r = x1^3*r;
aph_hat = k3*(1/m)*int_x3r;

u = m*e + m*ddotx1d + m*k1*(dotx1d - dotx1) + x1^3*aph_hat + k2*r;
ddotx1 = -(aph/m)*x1^3 + (1/m)*u;